天天速递!导数运算法则百度百科(导数运算法则推导过程)
时间:2023-06-02 02:13:04 来源:互联网
想必现在有很多小伙伴对于导数运算法则推导过程方面的知识都比较想要了解,那么今天小好小编就为大家收集了一些关于导数运算法则推导过程方面的知识分享给大家,希望大家会喜欢哦。
导数公式推导过程如下:
 (资料图片仅供参考)
(资料图片仅供参考)
y=a^x,△y=a^(x+△x)-a^x=a^x(a^△x-1),△y/△x=a^x(a^△x-1)/△x。
如果直接令△x→0,是不能导出导函数的,必须设一个辅助的函数β=a^△x-1通过换元进行计算。由设的辅助函数可以知道:△x=loga(1+β)
所以(a^△x-1)/△x=β/loga(1+β)=1/loga(1+β)^1/β。
显然,当△x→0时,β也是趋向于0的。而limβ→0(1+β)^1/β=e,所以limβ→01/loga(1+β)^1/β=1/logae=lna。
把这个结果代入lim△x→0△y/△x=lim△x→0a^x(a^△x-1)/△x后得到lim△x→0△y/△x=a^xlna。
可以知道,当a=e时有y=e^x y";=e^x。
常用导数:
y = C(C为常数) , y"; = 0。
y=xn, y"; = nxn-1。
y = ax, y"; = lna*ax。
y = ex, y"; = ex。
y = logax , y"; = 1 / (x*lna)。
y = lnx , y"; = 1/x。
y = sinx , y"; = cosx。
y = cosx , y"; = -sinx。
y = tanx , y"; = 1/cos2x = sec2x。
y = cotx , y"; = -1/sin2x= -csc2x。
y = arcsinx , y"; = 1 / √(1-x2)。
y = arccosx , y"; = - 1 /√(1-x2)。
y = arctanx , y"; = 1/(1+x2)。
导数运算法则推导过程
求函数y=f(x)在x0处导数的步骤:
① 求函数的增量Δy=f(x0+Δx)-f(x0)
② 求平均变化率
③ 取极限,得导数。
说得具体点,就是在函数上取相近的两点,求这两点的斜率,当这两点足够近时(取极限),所得的值就是函数在该点的导数。一般求导都是直接用导数公式(靠记忆)
用极限推导,在选修2-2里
(f(x)g(x))";
=im(x+h)v(x+h)-u(x)v(x)]/h}
=lin(x+h)v(x+h)-u(x)v(x+h)]/h}+LIM{[u(x)v(x+h)-u(x)v(x)]/h}
=u(x)";v(x)+u(x)v(x)";
[f(x)/g(x)]";
=lim(Δx→0)(f(x+Δx)/g(x+Δx)-f(x)/g(x))/Δx)
=lim(Δx→0)((g(x)*f(x+Δx)-f(x)*g(x+Δx))/(g(x+Δx)*g(x)))/Δx)
=lim(Δx→0)((g(x)*f(x+Δx)/Δx-f(x)*g(x+Δx)/Δx)/(g(x+Δx)*g(x)))
=lim(Δx→0)(g(x)*f(x+Δx)/Δx-f(x)*g(x+Δx)/Δx)/lim(Δx→0)(g(x+Δx)*g(x))
=lim(Δx→0){[g(x)*f(x +Δx)-g(x)*f(x)]/Δx+[g(x)*f(x)-f(x)*g(x+Δx)]/Δx}/lim(Δx→0)(g(x+Δx)*g(x))
=(f";(x)g(x)-f(x)g";(x))/(g(x))²
语音朗读:
标签:
最新文章推荐
- 陕西7名核酸检测阳性外省游客活动轨迹公布
- 万人说新疆 | 棉花朵朵赛白云,阿克苏美出新高度!
- 万人说新疆 | 孙芳红:我在新疆每天过得很充实也很快乐
- 万人说新疆 | 棉农阿卜来提开心地笑了
- 万人说新疆 | 阿迪力的棉花合作社年入300万
- 四川乐山犍为县发生4.3级地震 无人员伤亡
- 西安全面开展排查管控 目前20481人核酸检测结果均阴性
- 陕西7名核检阳性者为一旅行团同行人员 活动轨迹公布
- 西安交大举行2021级本科生迎新会 校长:学习是主动作为之事
- 【母亲河畔的中国】黄河岸边的这个村庄如何打好旅游服务牌?
X 关闭
资讯中心
 低价高品质引发抢购热潮 盒马生鲜奥莱在京靠什么赚钱?
低价高品质引发抢购热潮 盒马生鲜奥莱在京靠什么赚钱?
2022-07-08
 厦门保障性租赁房认定细则发布 配租面向新市民群体年度租金涨幅不超过5%
厦门保障性租赁房认定细则发布 配租面向新市民群体年度租金涨幅不超过5%
2022-05-20
2021-10-18
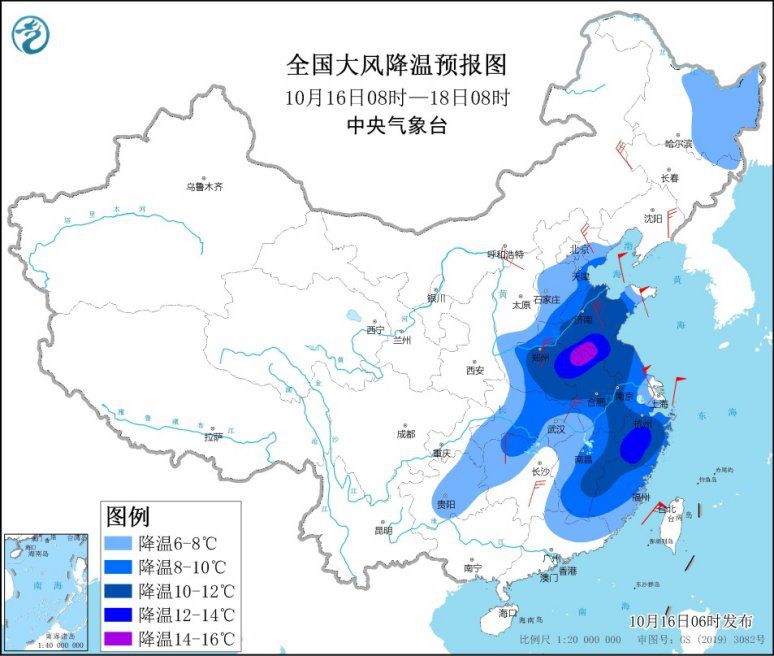 强冷空气继续影响中东部地区 局地降温14℃以上
强冷空气继续影响中东部地区 局地降温14℃以上
2021-10-18
X 关闭
热点资讯
-
1
天天速递!导数运算法则百度百科(导数运算法则推导过程)
-
2
环球今亮点!开封市龙亭区税务局:变“妆”办税服务厅 携“童”税宣未来行
-
3
天天观焦点:道指转涨 此前一度跌超200点
-
4
今日热讯:伤口结痂痒怎么办起泡(伤口结痂很痒怎么办)
-
5
2023陕西榆林市学生暑假放假时间
-
6
世界滚动:与时间赛跑 抢收抢晒小麦——豫南麦收区一线见闻
-
7
贾跃亭未履行总金额达87亿具体是什么情况
-
8
成交额逼近万亿大关!这一罕见现象暗藏投资机会?
-
9
【天天时快讯】@小军娃:不能陪你过节的爸爸发来节日祝福
-
10
车险“二次综改”来了!你的保费降了吗?
-
11
分支器与分配器的区别_分支器|当前滚动
-
12
四川卧龙:发现并命名5种植物新物种
-
13
塞尔达传说王国之泪孑然一身之战粉碎神庙挑战攻略一览
-
14
全球今热点:历史上秦琼的妻子是谁_历史上秦琼的老婆到底是谁呢简介介绍
-
15
组图丨“警”彩未来 “童”心守护
-
16
黛蛤散是什么 当前短讯
-
17
易成刚自体脂肪填充怎么样?隆胸技术如何?还在西京医院吗?
-
18
【世界时快讯】“帮人三忙,易惹是非”,老祖宗忠告:这三种忙千万不要帮,别等到吃亏才后悔
-
19
制止餐饮浪费非小事|天天最资讯
-
20
天天观焦点:中建八局津潍高铁2023年安全生产月启动仪式暨“安康杯”应急防汛演练顺利进行